As Time Goes By
Comparing the human experience of time with the fundamental tempos
of nature yields a startling new outlook on our place in the universe.
By Robert L. Jaffe
few years ago a geologist friend at M.I.T. gave me a small chunk of gneiss from Canada’s Northwest Territories. It rests now, backlit by the winter sun, on the windowsill behind my desk. A dull, fine-grained, gray-and-white rock, flecked with tiny crystals of black mica and hornblende, it looks like a stone she might have picked up almost anywhere in New England. Yet my stone is far from ordinary: its progenitor, the Acasta Formation, is the oldest known rock on Earth. The Acasta gneiss has persisted, largely undisturbed, at the core of North America since the rock crystallized more than 4 billion years ago, when the universe was only two-thirds its present age. The ripples in the gneiss on my windowsill have changed little in the billions of years since they formed. Meanwhile, great ranges of mountains have risen up and worn away; the lives of all our ancestors have flashed by. Occasionally I take the rock in my hand, trying in vain to capture some feeling for that vast expanse of time.
My fragment of gneiss holds other secrets as well. In spite of its outward calm, a microworld lies deep within, buzzing with incessant motion. Its tempo is set by its smallest parts: not the molecules of quartz and feldspar vibrating like miniature tuning forks; not the electrons whirling in orbits about the nuclear cores of atoms; not even the protons and neutrons churning within the nuclei. Rather, my bit of the Acasta gneiss beats time to the rhythm of quarks.
Whatever evanescent particles and subtle phenomena may await discovery, there is no doubt that we, and all we see around us, are made of quarks. Quarks account for 99.9 percent of the visible mass in the universe. Their orbits inside protons are exceedingly small, no more than a millionth of a millionth of a millimeter (10–15 meter) across, and their motions, which approach the speed of light, are exceedingly regular. Once around a proton takes a quark about 0.0000000000000000000001 (10–22) second, breathtakingly fast by any human measure. Just as the period of the Earth’s orbit around the Sun defines the year, so the time it takes a quark to complete one cycle of its motion in a proton defines one tick of the clock of fundamental physics. Those ceaseless motions of quarks mark the heartbeat of the universe.
One plain stone, two extraordinarily disparate landscapes of time: the cosmological, the billions of years over which the drama of the universe plays out; and the fundamental, the hectic pace at which elementary particles dance to the tune played by the laws of physics. Those are the natural rhythms of the world. Between the two extremes, far briefer than the grand sweep of cosmology, but far longer than the helter-skelter pace of fundamental processes, lie our human measures of time—the second, the day, the year. They are the times of our lives, but they are not the natural rhythms of the world. Where did they come from? Where do we fit in?
The answers have emerged from a journey of discovery that has created a second Copernican revolution. Five centuries ago, the first Copernican revolution dislodged humankind from our privileged position at the center of the universe. Quietly and relatively recently, particularly in the past half century, the way physical scientists think about time has undergone a similar revolution.
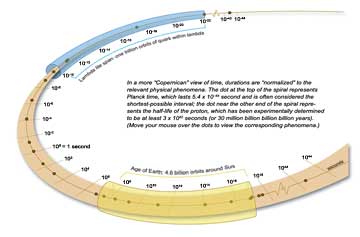
Observed for the briefest moments, nature’s forces turn out to have their own rhythms, built into them just as integrally as the clock speed of a microprocessor has been built into a computer at the factory. The smaller the part, the faster the tempo—but all of them are lightning quick compared to ordinary measures of human time. But if one suspends the attachment to human timescales, one can match the cinematographic frame speed of the mind’s eye to nature’s own rhythms, speeding up to capture the finest detail or slowing down to discern the broadest plan. The Copernican shift in perspective can be startling: the microworld, which seems so fleeting by human measures, instead persists languorously. The cosmos, which seems to define the eternal, instead roils with ceaseless change. [See illustration below.]
| ||
|
|
|
Then, late in the Renaissance, the Polish astronomer Nicolaus Copernicus rudely plucked us out of the center, placing the Sun, not the Earth, at the hub of the solar system. The astronomers who followed Copernicus moved our small planet out toward the periphery of a huge galaxy, teeming with stars like our own. They found the universe to be full of galaxies, ours no more exceptional than the others.
Today we can no longer claim a special place in the universe. But there are compensations. First, it is better to know the truth than to be deceived. Moreover, the drama of modern astronomy, though less personal, is far grander than it was before Copernicus. Stars form, then die, often in great explosions, and leave behind corpses of unimaginable density. Galaxies whirl and collide. Although our skies are no longer inhabited by just the likes of Orion the hunter and the Great Bear, the heavens are full of wonder for all to see, the rewards of surrendering our place at the center of the universe.
In the twentieth century we lost our bearings in time as utterly as our forebears in the Renaissance lost their special place in the universe. From the beginnings of civilization people have measured time in human-size intervals: in seconds, the beat of our hearts; in days, the apparent circling of the Sun and stars about us; in years, the cycles of the seasons.
Before the twentieth century, scientists and philosophers did not realize that nature might associate a clock speed with a particular force. Instead, the duration of phenomena seemed to vary according to the circumstances. Take celestial mechanics. Planets far from the Sun take longer to orbit than the ones close in. But the period of the orbit depends only on its size—the larger the orbit, the longer the period. In Newton’s law for calculating the force of gravity there is no constant that fixes the period of planetary orbits from the outset. Human measures of time may have seemed arbitrary, but they also were as good as any other.
Then, early in the twentieth century, revolutionary upheavals in physics led to the discovery that there are timescales intrinsic to the laws of physics themselves. Experimental physicists discovered that the mechanics of Newton is inadequate for describing the world of atoms. Newtonian mechanics was replaced by the strange and counterintuitive world of quantum mechanics, through which time entered physical law.
The German theoretical physicist Max Planck made the first key discovery in 1900. His study of radiant heat and light led him to conclude that, like ordinary water waves, those two forms of radiation vibrate, but that the radiation comes in packets, or “quanta.” Moreover, the energy of the quanta is directly proportional to the vibrating frequency of the light wave. Expressing the relation mathematically is as simple as relating the mass of a quantity of water in kilograms to the volume of the same quantity in cubic feet. If V is the volume in cubic feet, and M the mass in kilograms, then roughly M = 28 × V. Thus, the two quantities M and V vary in direct proportion, and they express related properties of the same substance. The more volume, the more mass. In this case the constant of proportionality, 28, is the density of water, the number of kilograms per cubic foot.
By the same token, if E is the energy of the radiation quanta in joules, and ν (the Greek letter nu) is the frequency of the quanta in vibrations per second, then Planck’s equation states that the two are proportional: the more energy, the higher the frequency of vibration. In this case the constant of proportionality is roughly 6.6 × 10–34 joule-second and, as Planck discovered, it is universal. The same constant of proportionality applies for heat radiation, for light, and even for X rays. That constant, usually abbreviated h, is known as Planck’s constant, and so the full statement of the proportion is E = h × ν. Standing with Einstein’s better-known E = mc², Planck’s equation is one of the twin pillars of modern physics.
Because Planck’s constant is so minute, when expressed in everyday units, even a modest energy equates to oscillations on an astonishingly short timescale. One quantum of green light, for instance, has only about 4 × 10–19 joule of energy, but that translates into about one oscillation every 2 × 10–15 second. A little human perspective: the “blink of an eye” takes about 50 trillion times longer.
It wasn’t until twenty-seven years after Planck’s original discovery about light that the implications of his law for other forms of energy and matter—and thus for nature’s fundamental timescales—became clear. The uncertainty principle articulated by the German physicist Werner Heisenberg provided the crucial link. The laws of quantum mechanics, Heisenberg realized, do not allow things to come perfectly to rest. It is impossible to know exactly where a particle is and, at the same time, where it is going. The more perfectly one tries to pinpoint the position of a particle, the more momentum, and therefore the more energy, it may have during the short time it occupies that position.
The uncertainty principle requires that everything on the microscale is constantly in a kind of perpetual, restless movement, a quantum buzz known as zero-point motion. And Planck’s equation determines the clock speed of zero-point motion: the smaller the system, the more precisely confined its position in space; the higher its energy; and, because E = h × ν, the faster the pulse of its zero-point motion.
Guided by quantum mechanics, twentieth-century physicists pushed deep into the microworld with ever more powerful instruments. Accelerators nearly the size of Manhattan have functioned as “microscopes” that could look for ever simpler, more fundamental processes, “listen” to ever faster tempos, and probe ever shorter timescales. When the physicists discovered new fundamental forces, such as the ones that hold electrons in atoms or quarks in protons, each force came with a natural clock speed, the pitch of the quantum buzz characteristic of the size of the system. All those clocks tick at frantic rates that make human intervals such as seconds, days, and years seem eternally long.
Freed from the constraint of viewing time in human terms, one can take a “Copernican journey” to find the tempos that rule the microworld. Imagine delving once more into my fragment of Acasta gneiss. This time, magnify the rock over and over again, just as you might repeatedly click the “+” button while you read a document on a computer.
| |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
The first few clicks resolve the pattern of flecks and ripples in the gneiss into jewel-like crystals, but betray no hints of time. More clicks, and patterns of striations within the crystals, the first hints of molecular substructure, come into focus. Still nothing moves. Not until the patterns begin to resolve into individual atoms, at the scale of nanometers (10–9 meter), do the faint, regular, self-sustaining vibrations of zero-point motion become detectable. The atoms vibrate ceaselessly back and forth with periods of about 10–13 second. Throughout that range, from rock to single atom, electromagnetic forces hold sway. They are the forces responsible for chemical binding and for the elementary processes of biology.
A few more clicks and individual atoms fill the screen, with hazy clouds of electrons orbiting atomic nuclei deep within. Electromagnetism still rules: the negatively charged electrons are held in orbit by their electrical attraction to the positively charged nucleus. Electromagnetism and quantum mechanics dictate both the period and size of the electrons’ orbits. An electron takes roughly 10–16 second to complete an orbit in a simple atom. Here at last is the beat of the electromagnetic force, the first of nature’s fundamental clocks.
With more clicks, the realm of electromagnetism begins to give way to more powerful forces. Five more powers of ten in magnification are needed to reach past the haze of electrons and resolve the seething mass of protons and neutrons in the atom’s nucleus. Only about 10–14 meter across, the nucleus accounts for nearly all the mass of the atom. Here another fundamental force, the strong force, emerges.
Although 100 times stronger than electromagnetism, the strong force is sequestered within atomic nuclei. It acts powerfully over distances less than 10–15 meter, typical of the distances between nuclear particles, but it rapidly becomes imperceptible as distances grow larger. At a range of 10–13 meter it is all but gone. The strong force holds protons and neutrons together in the nuclei of atoms. It fuels the nuclear fires that make stars shine, and also provides all the energy that makes life possible on Earth.
In its rawest form the strong force acts between quarks and confines them within protons and neutrons. Quarks (as far as physicists can determine) are indivisible bits of matter that carry “charges” somewhat like the electric charge of the electron. Quark charges come in three varieties, known whimsically as “colors.” Color charge is the source of the strong force, much the way electric charge is the source of the electromagnetic force. So the more accurate name for the strong force is the color, or “chromodynamic,” force.
Only inside protons and neutrons, at a distance of 10–15 meter, does the true tempo of the chromodynamic force come into focus. Confined to such minuscule spaces, quarks struggle mightily, but futilely, to escape. The regular, periodic zero-point motion of the quarks that results sets the tempo of the strong force: a single vibration, as I noted earlier, lasts about 10–22 second. That interval, which seems inconceivably short to us, beats the natural rhythm of the strong force.
The next stop on this Copernican journey, and the last where any new phenomena appear, comes into view at about 10–18 meter, one one-thousandth the size of the proton. At that distance another force—the weak force—becomes as strong as the electromagnetic force. The weak force is a bit like the fungus of the physics world: it does not build up very complex structures, it is easy to overlook, and it is often an agent of decay. When a nucleus disintegrates, it is usually the weak force at work. Because its effective range is limited to distances of one one-thousandth the size of the proton, the weak force only rarely affects the motions of quarks—and it is never the agent that binds matter together. So the beat of the weak force, even though it is a thousand times more rapid than the tempo of chromodynamics, is rarely heard in the universe.
The electromagnetic, strong, and weak forces dictate the structure of the microworld. Each has its own natural rhythm. The beats are dizzying: roughly 10–16, 10–22, and 10–25 second, respectively. But “dizzying” compared to what? It is time to take another leap of imagination, time to put aside the prejudice of a human perspective that sees the microworld as evanescent and its tempo as too fast. It is time to ask: What does the world of quarks look like on its own terms?
Consider one of the particles discovered in the early 1950s, known by the Greek capital letter lambda (Λ) because its telltale signature is a pair of tracks forming an upside-down letter V. Like the more familiar proton, the lambda is made of three quarks. From time to time one of the orbiting quarks in a lambda gets too close to one of the others—and within range of the weak force. When it does, the straying quark decays and the lambda flies apart. Lambdas live, on average, about one ten-billionth of a second (10–10 second), a typical life span for a subatomic particle that decays because of the weak interaction.
But is that really so short a time? Not if you take the Copernican leap, escape the human temporal perspective, and examine the lambda from the perspective of the strong force that holds it together. Though imperceptible to us, 10–10 second is a long, long time relative to the tempo of chromodynamics. It takes a quark about 10–22 second to complete a single orbit within the lambda. Before the lambda decays, the quarks within it orbit one another about 10–10 second divided by 10–22 second per orbit, or one trillion (1012) times, on average.
Nothing in our everyday experience lives so long in its own terms. Humanity’s most enduring institutions— churches, nations, universities—have lived at most hundreds of human lifetimes. Our most ancient ruins have survived only thousands of yearly cycles of heat and frost. Even the solar system is far less stable. Since its formation, the Earth has circled the Sun about 5 billion times. That is roughly 1/200th the comparable number for the lambda. In “only” another 5 billion years or so, the Sun will expire and take humanity, or what is left of it, along. Taking a fundamental, rather than a human perspective on time, high-energy physicists usually ignore the fact that the lambda decays at all, and call it “stable,” just like our solar system.
After this journey deep into my fragment of the Acasta gneiss, the word “stable” has taken on new significance. In the 4 billion years since this rock has formed, the quarks in it have orbited 1039 times—now that’s what I call stable! Hefting the stone in my hand, I find myself asking, What has enabled the universe to persist so long? If it were ruled by the tempos of the fundamental forces, one would expect the universe to have blinked into and out of existence in some tiny fraction of a second. What sets the immense scale of cosmological time? And what of gravity, which plays such a central role in cosmology?
Gravity, that most familiar of forces, has not figured in our search for the tempos of the microworld, because gravity is too weak to affect atoms or nuclei. Human beings are only aware of it because it reaches out across great distances and builds up when huge quantities of matter are gathered together. Because it plays such an important role in the dynamics of stars and galaxies, could gravity hold the key to understanding the scale of cosmological time? The question suggests another journey, this one across cosmic distances and exceedingly long times. But that’s a journey for another day.
Read more of Robert L. Jaffe’s exploration of time in “Times of Our Lives,” November 2006.
|
|
Copyright © Natural History Magazine, Inc., 2006